Figure 1. Given two triangle meshes $𝙰$ and $𝙱$, we find a continuous, bijective and low-distortion map between them (their edge images shown in (a)). Internally, we build a Compatible Intrinsic Triangulation (CIT), a pair of intrinsic triangulations on both models sharing the same connectivity; every vertex of $𝙰$ is inserted to $𝙱$’s intrinsic mesh, and vice versa (b). Our algorithm generates a piecewise-linear map in the form of overlay polygons; here, $𝙱$’s texture is being transferred to $𝙰$ with all the seams preserved (c).

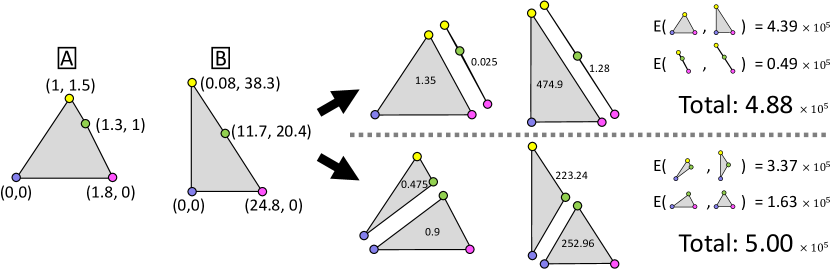
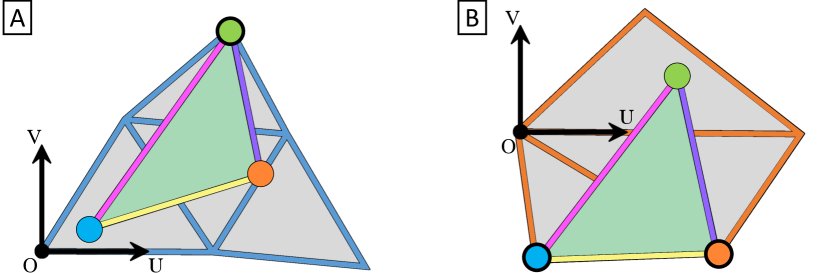
Compatible Intrinsic Triangulations

Abstract.

Finding distortion-minimizing homeomorphisms between surfaces of arbitrary genus is a fundamental task in computer graphics and geometry processing. We propose a simple method utilizing intrinsic triangulations, operating directly on the original surfaces without going through any intermediate domains such as a plane or a sphere. Given two models $𝙰$ and $𝙱$ as triangle meshes, our algorithm constructs a Compatible Intrinsic Triangulation (CIT), a pair of intrinsic triangulations over $𝙰$ and $𝙱$ with full correspondences in their vertices, edges and faces. Such a tessellation allows us to establish consistent images of edges and faces of $𝙰$’s input mesh over $𝙱$ (and vice versa) by tracing piecewise-geodesic paths over $𝙰$ and $𝙱$. Our algorithm for constructing CITs, primarily consisting of carefully designed edge flipping schemes, is empirical in nature without any guarantee of success, but turns out to be robust enough to be used within a similar second-order optimization framework as was used previously in the literature. The utility of our method is demonstrated through comparisons and evaluation on a standard benchmark dataset.

1. Introduction

Computing maps between surfaces is needed in many contexts, and has been a classical topic of great importance in computer graphics and geometry processing. In particular, maps that are continuous and bijective, called homeomorphisms, are required for many applications such as texture transfer and template fitting in order to avoid various kinds of artifacts, but at the same time they are generally more difficult to compute than other relaxed versions of maps.

Given two surfaces $𝙰$ and $𝙱$ as triangle meshes, a naive and intuitive idea one might think of is as follows:

1. map $𝙰$’s vertices onto $𝙱$ somehow, e.g., by using some form of projection, then

2. extend the above vertex-based map to $𝙰$’s edges and faces somehow, e.g., by using geodesics on $𝙱$.

If one pursued the above idea while working directly on the original surfaces, however, they would quickly realize that things get complicated. As such, all previous works introduce an intermediate domain such as a plane or a sphere and establish homeomorphisms by going through that intermediate domain. The method proposed by Schmidt et al. (2020) is the current state of the art in this area, where the surfaces are locally mapped to an intermediate domain in a globally consistent manner by using constant-curvature metrics. While their theory is elegant and results are impressive, their approach is conceptually not so intuitive, potentially making its implementation difficult for non-expert practitioners.

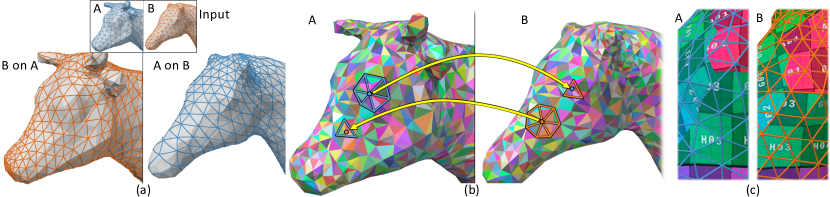
In this work, we present a simpler alternative that pursues the above intuitive idea using intrinsic triangulations (Sharp et al., 2019b) as our key ingredient. We propose Compatible Intrinsic Triangulation (CIT), a pair of intrinsic triangulations defined on $𝙰$ and $𝙱$ where the vertices, edges and faces are fully in correspondence (Fig. 1). Given vertex images as input, our algorithm constructs a CIT by employing carefully designed edge flipping schemes and other local operations (Sec. 4). CITs define strict homeomorphisms, and allow one to easily compute mapping distortions and their derivatives as well as to optimize the vertex images by using the similar second-order global optimization scheme as was used in the previous work (Schmidt et al., 2020) (Sec. 6).

We do not claim, however, any practical advantages over Schmidt et al. (2020)’s method. In fact, our method is less robust than theirs in the sense that it relies on the input vertex images being sufficiently high-quality; otherwise, our algorithm can fail, as discussed in Sec. 7. Nevertheless, to the best of our knowledge, our work is the first in the literature on computing surface homeomorphisms without going through any intermediate domains. In exchange for the conceptual simplicity and intuitiveness of our approach, we had to deal with a number of combinatorial problems which make our algorithm inherently empirical and heuristic, providing no guarantee for success. Yet, our algorithm is overall straightforward to implement, and we experimentally demonstrate practical level of robustness of our method using a standard benchmark dataset (Sec. 7.3).

We believe it is natural to utilize intrinsic triangulations for the purely intrinsic problem of inter-surface mappings. The two research domains have received increased attentions in the community recently, but only in separate, unrelated contexts. This work aims at bridging the two, thereby inspiring other researchers to develop new solutions to this difficult problem. In this light, we release our reference implementation at https://github.com/kenshi84/compatible-intrinsic-triangulations.

2. Related work

There are a large body of work on computing maps between surfaces, and they can be roughly divided into two groups based on whether strict homeomorphism is sought after or not. Those which do not seek for homeomorphism seem more popular, presumably because it is easier to represent and optimize maps in this setting. A variety of methods have been proposed including:

• projection-based methods (Ezuz et al., 2019a, b; Panozzo et al., 2013),

• distribution-based methods (Ovsjanikov et al., 2012; Solomon et al., 2012; Mandad et al., 2017), and

• methods developed in the context of surface registration (Huang et al., 2008; Bouaziz et al., 2013; Sharf et al., 2006; Tam et al., 2013; Wu et al., 2007; Yang et al., 2019, 2020; Zhang et al., 2006).

While there are many use cases for these relaxed maps, turning them into actual homeomorphisms is a non-trivial, open problem.

Computing homeomorphisms between surfaces is generally more difficult, and usually an intermediate domain is used in order to define the final map as a composition of individual maps between surfaces and the intermediate domain. Examples of intermediate domains include:

• a plane (Aigerman et al., 2014; Aigerman and Lipman, 2015; Aigerman et al., 2015; Kanai et al., 1997; Kim et al., 2011; Lipman and Funkhouser, 2009; Litke et al., 2005; Tierny et al., 2011; Schmidt et al., 2019),

• a sphere (Aigerman et al., 2017; Baden et al., 2018; Alexa, 2000; Asirvatham et al., 2005),

• a hyperbolic plane (Aigerman and Lipman, 2016; Shi et al., 2017), and

• base complexes (Praun et al., 2001; Schreiner et al., 2004; Kraevoy and Sheffer, 2004).

Among the above, only a very few address the problem of minimizing the map distortion in an end-to-end manner. Methods by Schreiner et al. (2004) and Kraevoy et al. (2004) only allow local optimization per each vertex’s 1-ring neighborhood, and are prone to converging to undesirable local minima. Methods by Litke et al. (2005) and Schmidt et al. (2019) do offer global optimization, but they are applicable only to surfaces of disk topology.

Distortion minimization of homeomorphisms between closed surfaces of arbitrary genus in a global and end-to-end manner was addressed only recently by Schmidt et al (2020). Our problem setting is exactly the same, and our results are similar with theirs. Unlike their method where surfaces are locally mapped to a respective intermediate domain (either a plane, a sphere, or a hyperbolic plane, depending on the surface genus) by using constant-curvature metrics, our method constructs consistent mappings between surfaces directly on the original surfaces without going through any intermediate domains by using intrinsic triangulations (Sharp et al., 2019b), which we believe leads to a simpler (albeit heuristic) algorithm.

Intrinsic triangulations

Our work is directly inspired by the powerful concept of intrinsic triangulations based on the signpost data structure (Sharp et al., 2019b), which has already found a number of extensions and use cases in the literature. Sharp and Crane (2020a) utilized it for defining a high-quality Laplacian operator on non-manifold meshes as well as point clouds. Sharp and Crane (2020b) also demonstrated that one can find polyhedral geodesics on surfaces by just flipping edges intrinsically. The intrinsic Delaunay triangulation algorithm has already been used for various geometry processing tasks (El Ouafdi et al., 2021; Fumero et al., 2020; Tao et al., 2021). Our work widens the application domains of intrinsic triangulations to the problem of inter-surface mappings.

Compatible triangulations for 2D animation

Our algorithm for constructing CITs is mainly about deciding which edges to flip based on the configuration of nearby vertices in a local 2D coordinate system, and thus is quite related to the existing literature on compatible triangulations in the context of 2D animation (Alexa et al., 2000; Surazhsky and Gotsman, 2004; Baxter III et al., 2009; Liu et al., 2018). Revisiting these algorithms in our context may lead to substantial improvement of our algorithm, which is left for future work.

Figure 2. The vertex insertion step (left) followed by the intrinsic Delaunay flipping step (right). Each vertex in correspondence is drawn in its unique color, and each original (i.e., non-inserted) vertex is drawn with a black silhouette. A merged vertex is drawn as a larger ball. The vertex highlighted by the red arrow originates in $𝙱$ and is inserted to $𝙰$’s input edge, splitting the two adjacent intrinsic faces. Each compatible edge (i.e., connecting the same pair of corresponding vertices) is drawn in its unique color, while each incompatible edge is drawn in dark gray. Notice how the intrinsic Delaunay flipping step reduces the number of incompatible edges significantly.

3. Overview

Our input consists of a pair of triangle meshes $M_{𝙰}=(V_{𝙰},E_{𝙰},F_{𝙰})$ and $M_{𝙱}=(V_{𝙱},E_{𝙱},F_{𝙱})$ for the two models, along with $𝙰$’s vertex image ${\varphi }_{𝙰\to 𝙱}:V_{𝙰}\mapsto F_{𝙱}\times \mathrm{\Lambda }$, with $\mathrm{\Lambda }=\{({\lambda }_1,{\lambda }_2,{\lambda }_3)|{\sum }_i{\lambda }_i=1\}\subset {ℝ}^3$ being the space of barycentric coordinates, which maps $𝙰$’s vertex to a point inside $𝙱$’s face, and the other one in the opposite direction ${\varphi }_{𝙱\to 𝙰}$. Any method of choice can be used to obtain these vertex images, such as the Hyperbolic Orbifold Tutte (HOT) method (Aigerman and Lipman, 2016); the only requirement is that they need to be reasonably consistent in both directions in order for our algorithm to succeed. Given such input data, our algorithm generates a Compatible Intrinsic Triangulation (CIT), as explained in Sec. 4.

In Sec. 5, we explain how to process the generated CIT further in order to obtain images of $E_{𝙰}$ on $M_{𝙱}$ and vice versa as piecewise-geodesic polylines, as well as the piecewise-linear mapping between $𝙰$ and $𝙱$ as an overlay mesh.

From the generated CIT, we compute the map’s distortion energy and its derivatives using automatic differentiation, just like the previous method (Schmidt et al., 2020). We displace the current vertex images by the computed descent direction multiplied by a certain step size, and plug them into our CIT generation algorithm again to arrive at a new configuration. We explain this optimization process in Sec. 6.

Notations

We use a bold font style to distinguish the intrinsic mesh and its elements from the input mesh and its elements on either model. For example, $v_{𝙰}\in V_{𝙰}$ refers to a vertex of $𝙰$’s input mesh, while ${𝐞}_{𝙱}\in {𝐄}_{𝙱}$ refers to an edge of $𝙱$’s intrinsic mesh.

4. CIT generation

4.1. Vertex insertion

After initializing intrinsic meshes ${𝐌}_{𝙰}$ and ${𝐌}_{𝙱}$ as copies of input meshes $M_{𝙰}$ and $M_{𝙱}$, we first insert $𝙰$’s input vertices $V_{𝙰}$ into ${𝐌}_{𝙱}$ according to the vertex image ${\varphi }_{𝙰\to 𝙱}$. For each input vertex $v_{𝙰}\in V_{𝙰}$, we check if its image ${\varphi }_{𝙰\to 𝙱}(v_{𝙰})=(f_{𝙱},𝝀)$ is strictly inside $f_{𝙱}$, i.e., if ${\lambda }_i>0,\forall i$ (we call such a mapped point a face point). If so, we insert a new vertex into an intrinsic face ${𝐟}_{𝙱}\in {𝐅}_{𝙱}$ corresponding to that face point, splitting ${𝐟}_{𝙱}$ into three.

If one component of $\{{\lambda }_i\}$ is zero, the mapped point is exactly on $𝙱$’s input edge $e_{𝙱}\in E_{𝙱}$ (we call such a mapped point an edge point). In this case, we insert a new vertex into an intrinsic edge ${𝐞}_{𝙱}\in {𝐄}_{𝙱}$ corresponding to that edge point, splitting ${𝐞}_{𝙱}$ into two.

If two components of $\{{\lambda }_i\}$ are zero, this means $𝙰$’s vertex $v_{𝙰}$ is mapped exactly onto $𝙱$’s vertex $v_{𝙱}$, i.e., ${\varphi }_{𝙰\to 𝙱}(v_{𝙰})=v_{𝙱}$. In this case, we ensure that the vertex image in the opposite direction is consistent, i.e., ${\varphi }_{𝙱\to 𝙰}(v_{𝙱})=v_{𝙰}$. We conceptually interpret such a case as the original vertex and the inserted vertex being merged in the intrinsic mesh, and we do not insert a new vertex in this case. In our method, we achieve hard constraints on a set of fixed corresponding vertex pairs by keeping them as merged (we call such fixed vertices anchors). If not using this hard constraints mode, we will later split each merged vertex into two (as explained in Sec. 4.7) in order to treat the two vertices as variables in the optimization.

Additionally, we introduce the following adjustment procedure for stability reasons: when all of $\{{\lambda }_i\}$ are positive but one component is extremely small, the mapped face point is almost on one of the edges of the mapped face. Having an intrinsic vertex at a face point extremely close to an input edge causes numerical instability for our overlay mesh extraction algorithm. As such, we clamp the smallest value below a threshold to zero and increase the other two components to sum to one, and treat it as an edge point.

We perform the same vertex insertion process in the opposite direction ($𝙱\to 𝙰$) as well.

Figure 3. Five subroutines constituting our FlipToCompatible algorithm.

4.2. Compatible edges & faces

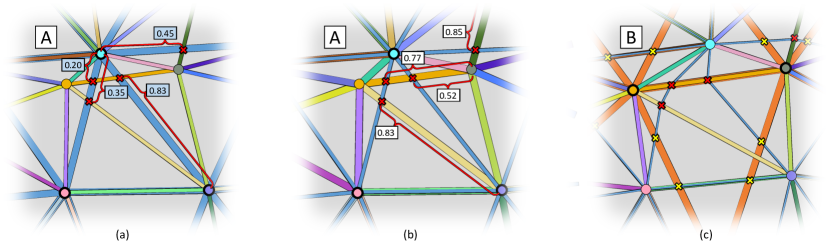
After the vertex insertion step, the intrinsic meshes ${𝐌}_{𝙰}$ and ${𝐌}_{𝙱}$ have the exact same numbers of vertices, edges and faces. Also, the intrinsic vertices of both models ${𝐕}_{𝙰}$ and ${𝐕}_{𝙱}$ are fully in correspondence. If the endpoints of $𝙰$’s intrinsic edge ${𝐞}_{𝙰}\in {𝐄}_{𝙰}$ correspond to the endpoints of $𝙱$’s intrinsic edge ${𝐞}_{𝙱}\in {𝐄}_{𝙱}$, we say ${𝐞}_{𝙰}$ and ${𝐞}_{𝙱}$ are compatible. If no such intrinsic edge in ${𝐄}_{𝙱}$ exists, we say ${𝐞}_{𝙰}$ is incompatible. We can further define the notion of face compatibility: if all the three edges of $𝙰$’s intrinsic face ${𝐟}_{𝙰}\in {𝐅}_{𝙰}$ are compatible, and if there exists $𝙱$’s intrinsic face ${𝐟}_{𝙱}\in {𝐅}_{𝙱}$ having the same set of compatible edges in the consistent order, then we say ${𝐟}_{𝙰}$ and ${𝐟}_{𝙱}$ are compatible. If ${𝐟}_{𝙱}$ has the same set of compatible edges but in the reversed order, we say ${𝐟}_{𝙰}$ and ${𝐟}_{𝙱}$ are reversed. If an intrinsic face is neither compatible nor reversed, we say it is incompatible. If all the intrinsic edges are compatible, all the intrinsic faces will be compatible by necessity. Our goal is to reach this state by mutating ${𝐌}_{𝙰}$ and ${𝐌}_{𝙱}$ in certain ways.

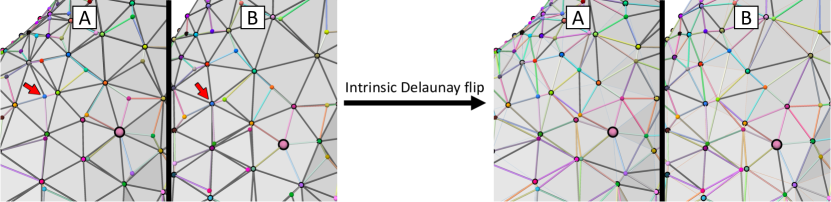
Fig. 2 left shows an example state after the vertex insertion step. We draw each vertex in correspondence as well as each compatible edge in their unique color, while we draw each incompatible edge in dark gray. Notice that only some fraction of the edges are compatible at this point.

There are some rules about intrinsic edges that must be adhered to in our algorithm: first, we do not allow self-edges, i.e., edges starting from and ending at the same vertex. We also do not allow multiple intrinsic edges connecting the same pair of intrinsic vertices, because they prevent the definition of one-to-one correspondence between $𝙰$’s intrinsic edge and $𝙱$’s intrinsic edge. These rules imply that every intrinsic vertex always has degree greater than two. In the following where we flip intrinsic edges, in addition to the geometric feasibility check in the original signpost method (Sharp et al., 2019b), we perform this uniqueness check in order to determine flippability of intrinsic edges.

4.3. Delaunay flipping

The first step in improving our meshes’ compatibility is to perform the intrinsic Delaunay flipping algorithm (Sharp et al., 2019b) on both intrinsic meshes ${𝐌}_{𝙰}$ and ${𝐌}_{𝙱}$ independently. When the input vertex images are reasonably consistent in both directions, the intrinsic vertices ${𝐕}_{𝙰}$ and ${𝐕}_{𝙱}$ tend to have vertex neighborhoods in similar geometric configurations, thus the Delaunay flipping procedures on both models tend to result in similar connectivities. Often, this step already makes a significant portion of the intrinsic edges compatible (Fig. 2 right).

4.4. Merging nearby vertices

An extremely short intrinsic edge in a CIT can be a source of numerical problems both for the computation of the energy derivatives and for the generation of the overlay mesh. The Delaunay flipping algorithm tends to have connected such nearby vertex pairs as compatible edges. Such extremely short intrinsic edges also tend to be collapsible, i.e., its endpoints consist of an original vertex and an inserted vertex, as they are usually caused by the input vertex images mapping $𝙰$’s vertex very close to $𝙱$’s vertex and vice versa.

As such, before proceeding to our main algorithm for improving compatibility as described below, we collapse each of such collapsible compatible edges whose length is below a threshold and turn them into a merged vertex. This edge collapse operation is realized by deleting the inserted vertex and reconnecting all of its adjacent edges to the original vertex.

4.5. FlipToCompatible algorithm

In this section, we describe our FlipToCompatible algorithm which tries to make ${𝐌}_{𝙰}$ and ${𝐌}_{𝙱}$ as compatible as possible by just flipping edges. Note that it is rare to obtain a valid CIT with this algorithm alone, especially when the input vertex images start to deviate from being mutually consistent (which happens when we examine large step sizes during optimization), and we will need to resort to some additional procedures that involve relocation of inserted vertices, as we explain later. We do prefer, however, to utilize edge flips maximally to improve compatibility, because we do not want to modify the input vertex images unnecessarily.

Our algorithm consists of five subroutines (Fig. 3), and it executes each of them in order. If a certain subroutine was able to increase the number of compatible edges, it goes back to the beginning and repeats until no more changes can be made. In the following, we explain each of the subroutines in the order of the more frequently applicable to the less frequent. The less frequent ones take effect only occasionally, but they do increase the chance of success of our CIT generation algorithm and are thus necessary.

Below, when deciding whether to flip an edge or not, we assume it is flippable (i.e., we ignore edges that are not flippable).

Subroutine 1: SimpleFlip

For $𝙰$’s incompatible edge ${𝐞}_{𝙰}\in {𝐄}_{𝙰}$, we check its opposite vertices, and if there is an incompatible edge ${𝐞}_{𝙱}\in {𝐄}_{𝙱}$ connecting these vertices, we flip ${𝐞}_{𝙰}$. We perform the same procedure in the opposite direction as well.

Subroutine 2: SimpleCoFlip

If there is a pair of incompatible edges ${𝐞}_{𝙰}$ and ${𝐞}_{𝙱}$ that have the same opposite vertices, we flip both of them.

Subroutine 3: FlipCompatible

Given a compatible edge ${𝐞}_{𝙰}^1$ and its counterpart ${𝐞}_{𝙱}^1$, we check if there is an incompatible edge ${𝐞}_{𝙱}^2$ that is either connecting ${𝐞}_{𝙰}$’s opposite vertices, or is flippable and has the same opposite vertices as ${𝐞}_{𝙰}^1$. We perform the same check in the opposite direction for ${𝐞}_{𝙱}^1$, and if the two checks both pass, we flip ${𝐞}_{𝙰}^1$ and ${𝐞}_{𝙱}^1$ (as well as ${𝐞}_{𝙱}^2$ (resp. ${𝐞}_{𝙰}^2$) if it has the same opposite vertices as ${𝐞}_{𝙰}^1$ (resp. ${𝐞}_{𝙱}^1$)).

Subroutine 4: FlipFlatPolygon

Sometimes, incompatible edges are clustered and form a patch of connected faces with no interior vertex. In such a case, all the faces in the patch can be flattened to 2D without any distortions, resulting in a pair of compatible 2D polygon boundaries for $𝙰$ and $𝙱$. Our algorithm tries to triangulate these two polygons in a compatible way. We use a simple heuristic to achieve this: for each vertex, we check if it is “visible” from each of all the other vertices of the polygon (i.e., the line segment between them is contained within the polygon) for both $𝙰$ and $𝙱$. If such a vertex is found, we connect all the other vertices to that found vertex by repeatedly flipping edges.

Figure 4. An example where FlipToCompatible is stuck (leftmost) but flipping one compatible edge pair within an incompatible patch (its boundary edges shown in red) leads to a different configuration (middle left) which can be handled by FlipToCompatible. The number above each arrow refers to the used subroutine of FlipToCompatible, while the number of incompatible edges in the patch is shown at the bottom of each figure.

Figure 5. Five patterns for merging inconsistently positioned vertices. Original and inserted vertices are drawn with thick and thin black silhouettes, respectively. The inserted vertex to be removed after the merge are highlighted by red arrows in each pattern.

Subroutine 5: DoubleFlipCompatible

For a pair of nearby compatible edges $({𝐞}_{𝙰}^1,{𝐞}_{𝙰}^2)$ and its counterpart $({𝐞}_{𝙱}^1,{𝐞}_{𝙱}^2)$, we flip all these four edges if the following conditions hold:

• ${𝐞}_{𝙰}^1$ and ${𝐞}_{𝙱}^2$ have the same opposite vertices.

• There is an incompatible edge ${𝐞}_{𝙱}^3$ that is connecting the opposite vertices of ${𝐞}_{𝙰}^2$.

• There is an incompatible edge ${𝐞}_{𝙰}^3$ that is connecting the opposite vertices of ${𝐞}_{𝙱}^1$.

4.6. Resolving incompatible patches

We define a connected set of non-compatible (i.e., reversed or incompatible) faces as an incompatible patch. At this point, assuming the input vertex images are reasonably consistent, we expect that the majority of edges have been made compatible and that there are small and sparsely distributed incompatible patches left. Our strategy then is to examine each of these incompatible patches and try to make them compatible by various means as explained below.

Note that a pair of incompatible patches in $𝙰$ and $𝙱$ can be made correspondent by checking if they consist of the same set of corresponding vertices. Thus, we extract all the corresponding pairs of incompatible patches and process each of them in order.

4.6.1. Exploring variations by flipping edges within patches

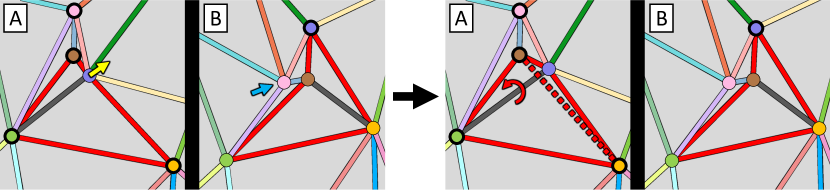
Consider an example incompatible patch shown in Fig. 4 at the far left where our FlipToCompatible algorithm cannot make any progress. It is, however, still possible to make FlipToCompatible process this patch if we flip the compatible edge pair highlighted by the red arrows in the figure. Note that flipping this edge pair does not increase the number of incompatible edges.

Based on this observation, after the termination of FlipToCompatible, for each corresponding pair of incompatible patches, and for each corresponding pair of their compatible edges, we check if flipping the edge pair preserves the number of incompatible edges. If so, we flip the edge pair and run FlipToCompatible again and see if it makes any progress, and if it does, we go back to the extraction of incompatible patches and repeat.

4.6.2. Merging inconsistently positioned vertices

After running our edge flipping algorithms as described above, there can still remain a few incompatible patches that cannot be resolved by just flipping edges. Such incompatible patches are often caused by the input vertex images mapping some vertex pairs close to each other on both $𝙰$ and $𝙱$, but in slightly inconsistent positions. Our next strategy then is to merge these vertices so that incompatible edges arising from them will disappear. We use a pattern-based approach for determining which vertex pair to merge, and we empirically identified five common patterns (Fig. 5). Note that for pattern 5 we relaxed the notion of face connectedness when extracting incompatible patches so that faces sharing only one vertex can be included in the same patch. See Appendix A for details about how we handle each pattern.

4.6.3. Deforming patch boundary

Figure 6. An example where our vertex merging algorithm cannot merge the purple and brown vertices due to the presence of the pink vertex on $𝙱$ (as highlighted by the blue arrow), since the line segment between the green and purple vertices crosses the cyan and orange edges adjacent to the pink vertex. In such a case, we move the purple vertex on $𝙰$ outwards a bit (as highlighted by the yellow arrow) to make the boundary shape of this incompatible patch convex, making its incompatible edge flippable (as highlighted by the red arrow).

Our vertex merging algorithm is sometimes unable to merge the intended vertices due to various configurations of vertices neighboring the incompatible patch, as illustrated in Fig. 6. In such cases, as a last resort, we try to deform the boundary shape of each incompatible patch so that it becomes convex, which will likely make some non-flippable incompatible edges flippable. Note that this operation can also fail due to various nearby vertex configurations. We run FlipToCompatible again if any of the patches could be deformed.

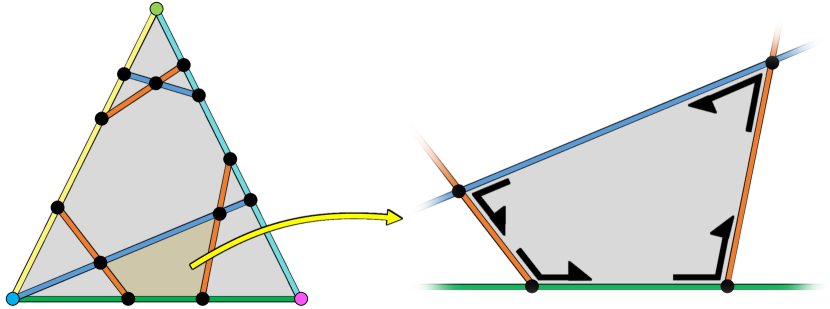
4.7. Splitting merged vertices

Figure 7. The split of a merged vertex. The pair of edges to be split is indicated by the red arrows, while the displacement vectors for the newly created vertex are indicated by the yellow arrows.

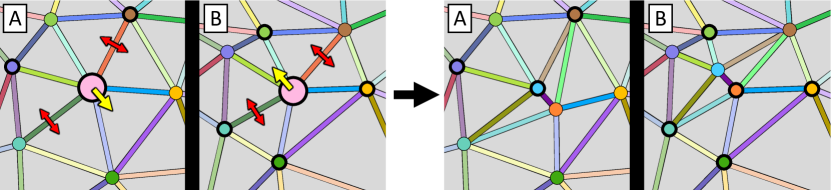
If there are any incompatible edges left at this point, our CIT generation algorithm has failed. Otherwise, we move to the next step of splitting merged (non-anchor) vertices (Fig. 7). To split a merged vertex, we first need to determine along which pair of edges the split should occur. We choose such a pair of edges (consistently across $𝙰$ and $𝙱$) in a way that makes the angle between the two edges as close to $\pi$ as possible. The newly created vertex is positioned at a point displaced from the original vertex in the average direction of the two edges and by a small distance (10% of the smallest height of the adjacent faces with the opposite edges being their bases). Note that the displacements on $𝙰$ and $𝙱$ should be opposite in order to maintain consistency.

4.8. Optimizing connectivity

Figure 8. An example where flipping edges to minimize the distortion energy can give rise to almost degenerate faces. A number inside or next to each triangle denotes its area.

Figure 9. The generation of images of $𝙰$’s original edges on $𝙱$’s input mesh. We first detect all the intersections of $𝙰$’s intrinsic edges against $𝙰$’s original edges, depicted as red crosses (a). The numbers in the blue boxes denote the relative arc-length parameter values of the intersections with respect to $𝙰$’s original edges. We then reinterpret these intersections as points on $𝙰$’s intrinsic edges, with their relative arc-length parameter values denoted by the numbers in the white boxes (b). Finally, we linearly map these points to $𝙱$’s intrinsic mesh, obtaining non-geodesic paths, and connect each pair of consecutive path points by a geodesic, obtaining piecewise-geodesic paths on $𝙱$’s input mesh (c). The yellow crosses denote intersections of these geodesic pieces and $𝙱$’s original edges, representing the intersections between $𝙰$’s edges and $𝙱$’s edges. We use line thickness to visualize different kinds of edges ($𝙰$’s original edges, $𝙱$’s original edges, and intrinsic edges), and we use the largest thickness to imply the underlying domain on which the geodesic paths are computed or defined.

Having succeeded in generating a valid CIT, we have a freedom to explore the space of CITs with various connectivities by flipping pairs of corresponding edges. A tempting strategy then, which we tried initially, is to repeatedly flip each edge pair if doing so results in lower energy, as per the Delaunay flipping algorithm (Sharp et al., 2019b), with an expectation that the final converged configuration will give the smoothest inter-surface map for a given vertex image. We realized, however, that this strategy has a serious issue: it does not care at all about the generation of almost degenerate faces (Fig. 8) which will cause numerical problems both in the computation of energy derivatives and the extraction of the overlay mesh.

As such, the strategy we adopted is to flip edges such that the smallest angle of corners of triangles on both $𝙰$ and $𝙱$ is maximized. While leading to a slightly higher energy, this approach generates much better quality triangles which makes our overall pipeline robust, and it tends to make the final edge and face images appear smoother, to our surprise. An in-depth analysis on the space of CITs by flipping edges is left for future work.

5. Obtaining piecewise-linear map

5.1. Obtaining edge images

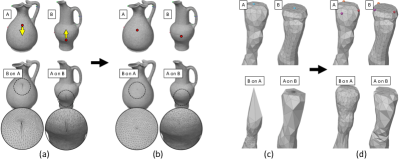
To obtain the piecewise-linear map induced by a CIT in the form of an overlay mesh, we first need to obtain images of $E_{𝙰}$ on $M_{𝙱}$ and vice versa, which tell us about where edges of $𝙰$ and $𝙱$ intersect. The process consists of three steps: first, we trace $𝙰$’s intrinsic edges ${𝐄}_{𝙰}$ over $𝙰$’s input mesh $M_{𝙰}$ to detect all their intersections with $𝙰$’s original edges $E_{𝙰}$, as was done in the original signpost method for visualizing intrinsic edges (Sharp et al., 2019b) (Fig. 9a). Next, we reinterpret the obtained intersections (edge points on $M_{𝙰}$) as edge points on ${𝐌}_{𝙰}$. This is easily done by calculating the relative arc-length parameter value of each intersection point with respect to the relevant intrinsic edge (Fig. 9b). Note that, by definition, a path corresponding to $e_{𝙰}\in E_{𝙰}$ on ${𝐌}_{𝙰}$ is always a geodesic. Finally, we linearly map such a path to $𝙱$’s intrinsic mesh ${𝐌}_{𝙱}$, obtaining a (generally) non-geodesic path on ${𝐌}_{𝙱}$, and connect its corresponding points on $M_{𝙱}$ by geodesics, obtaining a piecewise-geodesic path on $M_{𝙱}$ (Fig. 9c). The directions and distances for this final geodesic tracing are calculated based on the geometry of ${𝐌}_{𝙱}$. Intersections of this piecewise-geodesic path and $E_{𝙱}$ are recorded as intersections between $e_{𝙰}$ and $E_{𝙱}$.

We run the same process in the opposite direction to obtain images of $𝙱$’s original edges on $M_{𝙰}$. Note that this second run generates the same set of intersections between $E_{𝙰}$ and $E_{𝙱}$ up to small numerical errors.

Figure 10. (Left) Each intrinsic face can be intersected by any number of edges of $𝙰$ and $𝙱$, resulting in overlay polygons. (Right) We enumerate each overlay polygon by using a data structure called overlay wedge associated with each corner of the overlay polygon.

Figure 11. Overlay wedges generated per overlay vertex (depicted as a black circle at the center in each figure). (a) For an overlay vertex due to the intersection of two edges, we generate four overlay wedges. Here, $𝙰$’s original edge at index 123 and $𝙱$’s original edge at index 456 are intersected (with their canonical directions depicted as arrows). We use a common convention that an edge at index $n$ has its pair of halfedges at indices $2n$ and $2n+1$. (b,c,d) For an overlay vertex of the other types ($𝙰$’s vertex inserted into $𝙱$’s face, an anchor vertex where $𝙰$’s vertex and $𝙱$’s vertex overlap, and $𝙰$’s vertex inserted into $𝙱$’s edge, respectively), we generate overlay wedges according to the number of edges incident to the overlay vertex. Here, edges of the intrinsic mesh are depicted as thicker lines in various colors. Note that for (b) and (c), all the wedges have ${𝚝}_{\mathrm{𝙸𝙽}}=1$ and ${𝚝}_{\mathrm{𝙾𝚄𝚃}}=0$.

5.2. Overlay mesh generation

Having detected all the intersections between all possible pairs of edges, we are now ready to generate an overlay mesh for each of $𝙰$ and $𝙱$. As the two intrinsic meshes ${𝐌}_{𝙰}$ and ${𝐌}_{𝙱}$ are compatible, we no longer need to distinguish between them, so we drop the subscript in the following description when referring to the intrinsic mesh and its elements. Our goal is to enumerate all the overlay polygons in each intrinsic face $𝐟\in 𝐅$ which can be intersected by any number of $𝙰$’s original edges and $𝙱$’s original edges (Fig. 10 left). We achieve this using a data structure called an overlay wedge which is generated for each corner of an overlay polygon and encodes information about which halfedge to switch to when going around the overlay polygon (Fig. 10 right), as explained below.

We call each vertex in an overlay mesh an overlay vertex which can come from either

1. an intersection between edges (which can come from either $E_{𝙰}$, $E_{𝙱}$, or $𝐄$),

2. $𝙰$’s original vertex $V_{𝙰}$, or

3. $𝙱$’s original vertex $V_{𝙱}$.

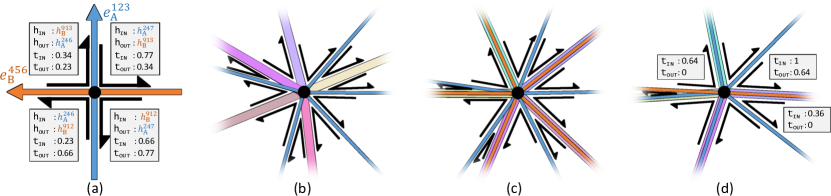
For the first case, we generate a quadruplet of overlay wedges for each intersection (Fig. 11a). An overlay wedge $𝚠$ stores a reference to the halfedge ${𝚑}_{\mathrm{𝙸𝙽}}$ which comes into the corner when viewed from inside its associated overlay polygon (assuming the counterclockwise ordering), along with the relative arc-length parameter value ${𝚝}_{\mathrm{𝙸𝙽}}$ representing the position of the intersection on ${𝚑}_{\mathrm{𝙸𝙽}}$. Note that ${𝚑}_{\mathrm{𝙸𝙽}}$ can refer to either the intrinsic mesh’s halfedge $𝐡$, $𝙰$’s original halfedge $h_{𝙰}$, or $𝙱$’s original halfedge $h_{𝙱}$. Likewise, $𝚠$ also stores a reference to the outgoing halfedge ${𝚑}_{\mathrm{𝙾𝚄𝚃}}$ and its associated parameter value ${𝚝}_{\mathrm{𝙾𝚄𝚃}}$.

For the other two cases, we generate a number of overlay wedges according to the number of edges incident to the overlay vertex (Fig. 11b-d). To do so, we first need to determine the correct ordering of halfedges incident to the overlay vertex originating from different sources ($M_{𝙰}$, $M_{𝙱}$, or $𝐌$), which is possible thanks to the signpost data structure storing directions of intrinsic edges relative to the canonical tangent spaces defined on vertices, edges, and faces of the input mesh (Sharp et al., 2019b).

Having processed all the overlay vertices and generated all the overlay wedges, we group them by their ${𝚑}_{\mathrm{𝙸𝙽}}$ fields, and for each group, we sort them by their ${𝚝}_{\mathrm{𝙸𝙽}}$ values. This allows us to find, given an overlay wedge $𝚠$, its “next” overlay wedge in the overlay polygon by the following procedure:

1. obtain the sorted list of wedges associated with $𝚠.{𝚑}_{\mathrm{𝙾𝚄𝚃}}$, and

2. scan the list in the ascending order and return the first item whose ${𝚝}_{\mathrm{𝙸𝙽}}$ value is greater than $𝚠.{𝚝}_{\mathrm{𝙾𝚄𝚃}}$.

This way, we can find cycles of overlay wedges and thus generate overlay polygons.

Also, because each overlay wedge stores references to halfedges of the input meshes, we can transfer the texture coordinate data present in the original meshes (which are typically stored per halfedge) to the overlay meshes. This allows us to transfer a texture image from one model to the other while preserving all the seams, as demonstrated in Fig. 1c.

6. Optimization

Figure 12. Flattening of ${𝐟}_{𝙰}$’s support patch (left) and ${𝐟}_{𝙱}$’s support patch (right) for the computation of the energy derivative. Note that the orange vertex which originates in $V_{𝙱}$ is inserted into $e_{𝙰}\in E_{𝙰}$, and we need to include its adjacent face not overlapping with ${𝐟}_{𝙰}$ in the patch because it is used as the tangent space for that edge point.

6.1. Computing energy & derivatives

Given a CIT, computing its distortion energy (measured using the symmetric Dirichlet as was done in the previous work (Schmidt et al., 2019, 2020)) is simple if it were not for its derivative computation: the intrinsic edge lengths already define the 2D shape of each intrinsic face, so we can trivially compute the energy using these 2D shapes:

(1) $$ℰ=\sum _{𝐟\in 𝐅}{\Vert 𝐉(𝐟)\Vert }_{\mathrm{F}}^{2}Area({𝐟}_{𝙱})+{\Vert 𝐉{(𝐟)}^{-1}\Vert }_{\mathrm{F}}^{2}Area({𝐟}_{𝙰})$$

where $𝐉(𝐟)=𝐃({𝐟}_{𝙱})𝐃{({𝐟}_{𝙰})}^{-1}\in {ℝ}^{2\times 2}$ is a map Jacobian deforming ${𝐟}_{𝙰}$ into ${𝐟}_{𝙱}$ in an arbitrary 2D embedding, $𝐃({𝐟}_{𝙰})=[{𝐩}_2-{𝐩}_1,{𝐩}_3-{𝐩}_1]\in {ℝ}^{2\times 2}$, and ${𝐩}_1,{𝐩}_2,{𝐩}_3\in {ℝ}^2$ are the embedded 2D coordinates of ${𝐟}_{𝙰}$’s three corners ($𝐃({𝐟}_{𝙱})\in {ℝ}^{2\times 2}$ is defined analogously). We use this lightweight method to compute the energy during the line search as described in Sec. 6.2.

To compute the derivative, however, we need to express the energy as a function of the input vertex images $ℰ({\varphi }_{𝙰\to 𝙱},{\varphi }_{𝙱\to 𝙰})$, which boils down to expressing those embedded 2D coordinates of intrinsic faces’ corners (i.e., ${𝐩}_1,{𝐩}_2$ and ${𝐩}_3$ introduced above) as linear combinations of 2D coordinates of $V_{𝙰}$ or $V_{𝙱}$ locally embedded in 2D. For example, suppose one corner of $𝐟\in 𝐅$ originates in $v_{𝙱}\in V_{𝙱}$ and is mapped to a face point on $M_{𝙰}$ as ${\varphi }_{𝙱\to 𝙰}(v_{𝙱})=(f_{𝙰},({\lambda }_1,{\lambda }_2,{\lambda }_3))$ where ${\lambda }_1>0$, ${\lambda }_2>0$ and ${\lambda }_3=1-{\lambda }_1-{\lambda }_2>0$. Then, we need to express the 2D coordinate of the corresponding corner of ${𝐟}_{𝙰}$ as a function of ${\lambda }_1$ and ${\lambda }_2$:

(2) $$𝐩({\lambda }_1,{\lambda }_2)={\lambda }_1{𝐪}_1+{\lambda }_2{𝐪}_2+(1-{\lambda }_1-{\lambda }_2){𝐪}_3$$

where ${𝐪}_1,{𝐪}_2$ and ${𝐪}_3$ are the 2D coordinates of $f_{𝙰}$ embedded in 2D locally. Note that this local embedding (or flattening) must be consistent (i.e., in a common coordinate frame) among all the original faces $\{f_{𝙰}\}\subset F_{𝙰}$ that support ${𝐟}_{𝙰}$ (we call this face set ${𝐟}_{𝙰}$’s support patch, see Fig. 12 left). This is always possible without introducing any distortions thanks to the construction of intrinsic triangulations guaranteeing nonexistence of original vertices inside any of intrinsic faces (Sharp et al., 2019b).

Note that when ${\varphi }_{𝙱\to 𝙰}(v_{𝙱})$ is an edge point, we use one of the edge’s two adjacent faces (determined by the edge’s canonical orientation) as the tangent space and reinterpret the edge point as a face point in that face. For this reason, ${𝐟}_{𝙰}$’s support patch must include such an adjacent face even if it does not overlap with ${𝐟}_{𝙰}$ (see the bottom right triangle of ${𝐟}_{𝙰}$’s support patch in Fig. 12 left).

We perform the same procedure for ${𝐟}_{𝙱}\in {𝐅}_{𝙱}$ corresponding to ${𝐟}_{𝙰}$ (Fig. 12 right), and derive the energy expression as a function of all the barycentric coordinates of the input vertex images involved in this intrinsic face. In the absence of anchor vertices, each corner of an intrinsic face corresponds to an inserted vertex in one model and to an original vertex in the other model, so each corner has two degrees of freedom, and each intrinsic face has six degrees of freedom. The existence of an anchor vertex decreases the degrees of freedom by two.

We use automatic differentiation to compute a local gradient vector ${𝐠}_{𝐟}\in {ℝ}^6$ and a Hessian matrix ${𝐇}_{𝐟}\in {ℝ}^{6\times 6}$ per intrinsic face $𝐟\in 𝐅$. These local quantities are accumulated in a global gradient vector $𝐠\in {ℝ}^n$ and a Hessian matrix $𝐇\in {ℝ}^{n\times n}$ where $n=2(|V_{𝙰}|+|V_{𝙱}|)$ in the absence of anchor vertices. As in the previous work (Schmidt et al., 2019, 2020), we make the global Hessian $𝐇$ positive definite by clamping negative eigenvalues of the local Hessian ${𝐇}_{𝐟}$ before accumulating.

6.2. Overall scheme

We basically adopt the same second-order optimization scheme as in the previous work (Schmidt et al., 2019, 2020):

• We temporally smooth the gradient as $\overline{𝐠}={\sum }_{i=0}^5{2}^{-i}{𝐠}_i$ where ${𝐠}_i$ is the gradient of the configuration $i$ steps previous to the current one. Temporally smoothed Hessian $\overline{𝐇}$ is obtained analogously.

• We compute the descent direction $𝐝\in {ℝ}^n$ by solving

  (3) $$(\overline{𝐇}+w_{\mathrm{L}}{(\mathrm{𝐒𝐋})}^{\top }\mathrm{𝐌𝐒𝐋})𝐝=-\overline{𝐠}$$

  where $w_{\mathrm{L}}$ is a weight for the Laplacian preconditioning, $𝐋$ is the connection Laplacian, $𝐒$ is a block-diagonal matrix responsible for making the tangent vector magnitudes comparable, and $𝐌$ is the diagonal mass matrix.

• We perform a line search by evaluating the energy at $𝐱+s𝐝$ where $𝐱\in {ℝ}^n$ is the current configuration (i.e., barycentric coordinates in the vertex images) and $s>0$ is the step size.

Because our variables are barycentric coordinates, all of the above are realized through the concept of tangent vector transport; please refer to Section 1 of the supplementary material of (Schmidt et al., 2020) for more details.

As opposed to the previous method which determined the feasibility of a given step size by the emergence of flipped triangles, we deem a given step size to be feasible if our CIT generation algorithm succeeds with it. When determining the maximum step size $s_{\max }$ for the line search, we initialize it based on the current descent direction vector (we set $s_{\max }=0.01/d_{\max }$ where $d_{\max }$ is the largest length of the 2D descent direction vectors after being scaled from the barycentric coordinates to the comparable lengths). If this initial value turns out to be feasible, we enter the upward mode where we multiply $s_{\max }$ by 1.2 and see if the increased $s_{\max }$ is infeasible. Otherwise, we enter the downward mode where we divide $s_{\max }$ by 1.2 and see if the decreased $s_{\max }$ is feasible. With $s_{\max }$ determined, we look for the optimal step size satisfying the Armijo condition as was done in the previous method.

6.3. Dealing with local minima

Our method lacks one important feature that existed in the previous method (Schmidt et al., 2020): the metric regularization. It was used in the initial few hundred steps to smooth out excess distortions in the input maps, and we believe this contributed greatly to the robustness of their optimization algorithm. In our case, unfortunately, we do not have anything that has the same effect as the metric regularization, and thus our optimization algorithm can easily get trapped by local minima, as discussed in Sec. 7.1.

We found empirically that when we get stuck in a local minimum, it is often possible to make (sometimes great) progress if we switch to the first-order optimization scheme. The reason we speculate is that the energy landscape can sometimes get very non-smooth with steep peaks and dents, making the quadratic approximation of the second-order optimization scheme a poor fit. As such, we devised the following simple workaround: we start with the second-order mode, and when we get stuck in a local minimum, we switch to the first-order mode and keep moving until we get stuck again in another local minimum, then we switch back to the second-order mode and repeat, until we get stuck in both schemes.

7. Results

Implementation and setup.

We implemented our algorithm using geometry-central (Sharp et al., 2019a) that includes the reference implementation of the signpost data structure (Sharp et al., 2019b). We used an unsupported module in Eigen (Guennebaud et al., 2010) for automatic differentiation. We ran all the experiments on Ryzen 9 3900X with 32GB of RAM running Ubuntu 20.04.1 LTS, and we always used a single thread during the optimization. We normalized the given input triangle meshes such that their total surface areas equal to one, meaning that the best attainable energy is 4.0. As opposed to the previous work, we did not impose any limit on the number of the optimization steps and let the algorithm run until it gets stuck (we stopped the optimization when the energy decrease fell below ${10}^{-5}$).

7.1. Initial map generation

To create the initial vertex images, we used the reference implementation of HOT (Aigerman and Lipman, 2016) and our own implementation of Seamless Surface Mappings (SSM) (Aigerman et al., 2015) (which we will release at https://github.com/kenshi84/seamlesssurfmap) for genus 0 cases and high genus cases, respectively. Because the success of our CIT generation/optimization algorithm depends heavily on the quality of the initial map, we allowed ourselves to use as many landmarks as necessary to produce good quality maps.

While theoretical analysis of exact conditions for the success of our CIT generation/optimization algorithm is left for future work, empirically we found some tips on how to place landmarks in an effective way. First, common to HOT and SSM, the mapping distortion tends to concentrate near landmarks; in particular, a landmark, when mapped to the other surface, may appear as if it was “pinched” in a certain direction (Fig. 13a). For a vertex image where this pinching effect is very strong, our CIT generation tends to fail. In such cases, we slightly shift those problematic landmarks toward the opposite of the pinched direction (Fig. 13b).

Second, when mapping an elongated part, if we placed just one landmark at the tip of the part, its nearby vertices, when mapped to the other surface, may often get severely concentrated or dispersed (Fig. 13c). Even though our CIT generation algorithm often succeeds with such a vertex image, our CIT optimization algorithm often gets stuck in a local minimum, unable to distribute those vertices evenly. To avoid this, we add a few more landmarks near the tip of the part so that the vertex distribution becomes more even (Fig. 13d). See the supplemental material for our choices of landmarks.

Figure 13. Tips on placing landmarks. “B on A” visualizes the vertex image ${\varphi }_{𝙱\to 𝙰}$ as a mesh $({\varphi }_{𝙱\to 𝙰}(V_{𝙱}),E_{𝙱},F_{𝙱})$, and vice versa. Mapping distortion concentrated near a landmark may appear as if the landmark was “pinched” in a certain direction (a), and this may cause our CIT generation algorithm to fail. This can be remedied by shifting the landmark toward the opposite of the pinched direction (b). Placing just one landmark at the tip of an elongated part may lead to too uneven distribution of mapped vertices (c), which may cause our CIT optimization algorithm to get stuck in a local minimum. To avoid this, we place a few more landmarks (d).

7.2. Comparison to Schmidt et al. (2020)

We ran our method on the dataset released by Schmidt et al. (2020) and compared the final distortion energy (see Fig. 14 for the final optimized maps). As shown in Table 1, our optimized distortion energy is below that of the previous method (Schmidt et al., 2020) on all but the Ant-Octopus and Pig-Armadillo cases. We believe the lower values of our energy are due to the fact that Schmidt et al. terminated optimization after a fixed number of steps, whereas we let the optimizer run until it can make no more progress. The two unsuccessful cases are of extremely non-isometric shape pairs, and our algorithm quickly gets trapped by local minima.

Figure 14. Optimization results on the dataset of (Schmidt et al., 2020).

Table 1. The result statistics. #F refers to the total number of triangles of the input triangle mesh pair, #N refers to the number of optimization steps taken, T refers to the total time taken for the optimization, and E refers to the energy of the optimized map. The energy of the map generated by the previous method is shown in the rightmost column.

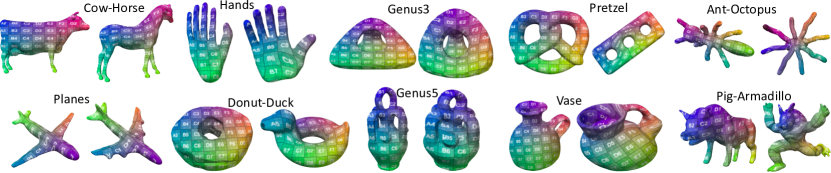
Case name	#F	#N	T	E	(Schmidt et al., 2020)
Planes	25k	231	15.0h	4.35	4.69
Cow-Horse	10k	225	3.8h	4.73	5.28
Hands	32k	366	37.6h	4.35	4.83
Genus3	3k	440	2.9h	4.21	4.36
Genus5	8k	767	15.0h	4.49	4.74
Pretzel	12k	532	11.2h	5.25	5.53
Donut-Duck	24k	585	78.9h	4.68	4.77
Vase	10k	542	9.1h	4.60	5.00
Ant-Octopus	8k	4	1m	98.3	16.2
Pig-Armadillo	22k	370	19.9h	8.10	7.78

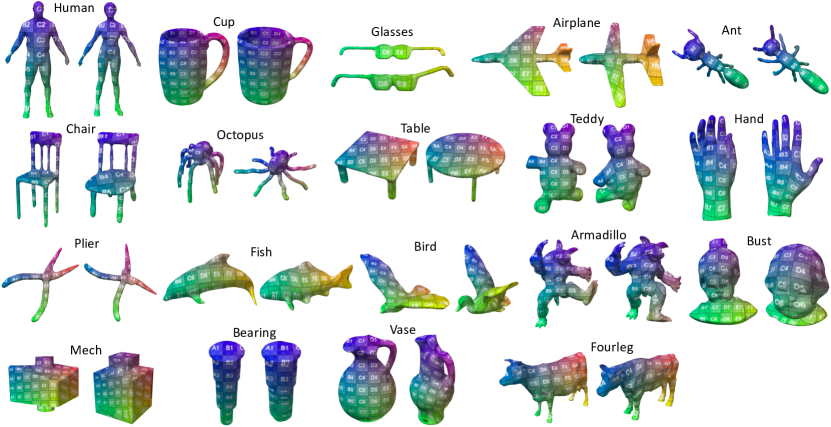
7.3. Evaluation with Princeton Segmentation Dataset

Our method is inherently empirical, hence it is difficult to theoretically analyze how well it works in practice. To evaluate practical utility of our method, we ran our CIT optimization on models included in the Princeton 3D Mesh Segmentation Dataset (Chen et al., 2009). The dataset consists of 19 categories, each containing 20 triangle meshes. We randomly chose 5 pairs in each category, totaling $19\times 5=95$ pairs. To make our experiment more meaningful, we created some rules to filter out some clearly inappropriate pairs as well as extremely poor quality geometries. In some categories, we also introduced some additional sub-categories within which we formed pairs randomly, so that the problem setting becomes more relevant. See the supplemental material for how we selected the pairs. Note also that we often applied moderate degree of mesh cleaning such as remeshing and reduction to eliminate erroneous configurations such as edges of almost zero dihedral angles.

Fig. 15 shows a sample of our optimized surface mapping from each category, indicating that our method indeed produces good quality maps. See the supplemental material for the detailed statistics as well as all the images of the mappings of all pairs.

Of the 95 cases, 7 cases (41-59, 50-46, 53-54, 55-51, 124-139, 146-156, 399-385), all genus 0, could not be handled by HOT (due to flipped triangles detected during its LBFGS optimization), no matter how we chose the landmarks. Out of the remaining 88 cases, we had 7 cases (62-72, 128-136, 129-126, 130-134, 152-149, 220-201, 386-397) where our CIT generation algorithm failed due to too extreme distortion in the mapping generated by HOT (Fig. 16). For the two cases 62-72 and 386-397, the shapes are widely different near the tail region, while for the two cases 152-149 and 220-201, the overall shapes are very different. For the three cases 128-136, 129-126 and 130-134, the very thin and long tentacles of the octopuses are arranged in some inconsistent manner.

Figure 15. Sample optimized maps from our experiment on the Princeton Segmentation Dataset.

Figure 16. 7 cases where our CIT generation algorithm failed..

Apart from these rather extreme cases, our CIT generation and optimization algorithm succeeded on 81 models out of 88, giving us success rate of 92%.

8. Conclusion and future work

In this work, we showed that it is possible to consistently define, given vertex images as input, images of edges and faces of one model onto the other model using Compatible Intrinsic Triangulations instead of constant-curvature metrics (Schmidt et al., 2020). We demonstrated that our CIT generation algorithm is robust enough to be used within a second-order global optimization framework.

There are, however, a number of issues in our current approach. First, there are no theoretical grounds supporting our CIT generation algorithm which we devised only through empirical observations. A thorough analysis of our problem setting is essential and can be a key to improving the robustness when handling extremely distorted vertex images.

One possible idea for improving our algorithm’s success rate is to introduce additional vertices which are both inserted on ${𝐌}_{𝙰}$ and ${𝐌}_{𝙱}$, much like the Steiner vertices for 2D triangulation. We have not tried it yet as it seemed to complicate our optimization framework due to the number of variables changing at every step, especially when considering the treatment of the temporal smoothing operator.

Another possible way of improvement would be to devise a mechanism that has the same effect as the metric regularization feature in the previous work (Schmidt et al., 2019, 2020) which we believe will make our optimization algorithm significantly more robust.

Finally, an interesting future direction would be to combine our method with recent techniques for computing bijective maps between coarse and fine meshes such as (Jiang et al., 2020), in order to enable a multi-resolution framework for the inter-surface mapping problem. This will benefit from the simplicity of our approach, requiring only vertex images as input, in contrast to the previous method which requires valid constant-curvature metrics in addition to vertex images.

Appendix A Algorithms for merging inconsistently positioned vertices

We match the given incompatible patch pair against each of the five patterns shown in Fig. 5. Each pattern analyzes the given patch pair and returns an edge pair (one on ${𝐌}_{𝙰}$ and the other on ${𝐌}_{𝙱}$) that meets certain conditions defined for that pattern. We then collapse such a returned edge pair if it is collapsible. We give up on a patch pair if none of the patterns return an edge pair for collapse.

Below, we use ${\mathit{\varphi }}_{𝙰\to 𝙱}$ and ${\mathit{\varphi }}_{𝙱\to 𝙰}$ to refer to the available correspondences between ${𝐌}_{𝙰}$’s elements and ${𝐌}_{𝙱}$’s elements; e.g., ${𝐯}_{𝙱}={\mathit{\varphi }}_{𝙰\to 𝙱}({𝐯}_{𝙰})$ refers to $𝙱$’s intrinsic vertex corresponding to $𝙰$’s intrinsic vertex (which is always available), and ${𝐞}_{𝙰}={\mathit{\varphi }}_{𝙱\to 𝙰}({𝐞}_{𝙱})$ refers to $𝙰$’s intrinsic edge corresponding to $𝙱$’s intrinsic edge, assuming that the edge is compatible.

Pattern 1

We first check if the patch contains no interior vertices. We then look for vertices whose interior angle (i.e., the sum of corner angles of adjacent faces in the patch) is larger than $\pi$. If $𝙰$’s patch and $𝙱$’s patch contain one such vertex each (referred to as ${𝐯}_{𝙰}$ and ${𝐯}_{𝙱}$, respectively), and if there exists an edge at $𝙰$’s patch boundary connecting ${𝐯}_{𝙰}$ and ${\mathit{\varphi }}_{𝙱\to 𝙰}({𝐯}_{𝙱})$, we return that edge.

Pattern 2

We first check if the patch contains just one interior vertex ${𝐯}_{𝙰}$ and just one reversed face ${𝐟}_{𝙰}$. We also check if ${𝐯}_{𝙰}$ is adjacent to ${𝐟}_{𝙰}$. Then we examine the two edges ${𝐞}_{𝙰}^1$ and ${𝐞}_{𝙰}^2$ adjacent to both ${𝐯}_{𝙰}$ and ${𝐟}_{𝙰}$. We return ${𝐞}_{𝙰}^1$ if , otherwise ${𝐞}_{𝙰}^2$, with $|\cdot |$ representing the edge’s length.

Pattern 3

We first check if the patch contains even number of interior vertices. Then, we look for an interior compatible edge pair ${𝐞}_{𝙰}$ and ${𝐞}_{𝙱}$ whose adjacent two faces are both reversed. If the adjacent vertices of ${𝐞}_{𝙰}$ and ${𝐞}_{𝙱}$ are all interior, we return ${𝐞}_{𝙰}$. Otherwise, if ${𝐞}_{𝙰}$ and ${𝐞}_{𝙱}$ are both flippable and have corresponding opposite vertices which are both interior, we flip both of them and return ${𝐞}_{𝙰}$.

Pattern 4

We first check if the patch contains no interior vertices. We then look for an interior compatible edge pair ${𝐞}_{𝙰}$ and ${𝐞}_{𝙱}$ whose adjacent vertices all have interior angles larger than $\pi$. If there is just one such edge pair in the patch, we return that edge.

Pattern 5

We match the given patch with the fixed mesh topology shown in the figure; i.e., the patch must have four faces, three interior edges, six boundary edges, five boundary vertices, and one interior vertex. We then identify the “hourglass” vertex; i.e., one that is adjacent to four boundary edges. Then we return an edge between the interior vertex and the hourglass vertex.